初中数学：最短路径求最值12个模型详解，掌握了 - 数学教育学报杂志社投稿

一、稿件要求： 1、稿件内容应该是与某一计算机类具体产品紧密相关的新闻评论、购买体验、性能详析等文章。要求稿件论点中立，论述详实，能够对读者的购买起到指导作用。文章体裁不限，字数不限。 2、稿件建议采用纯文本格式(*.txt)。如果是文本文件，请注明插图位置。插图应清晰可辨，可保存为*.jpg、*.gif格式。如使用word等编辑的文本，建议不要将图片直接嵌在word文件中，而将插图另存，并注明插图位置。 3、如果用电子邮件投稿，最好压缩后发送。 4、请使用中文的标点符号。例如句号为。而不是.。 5、来稿请注明作者署名(真实姓名、笔名)、详细地址、邮编、联系电话、E-mail地址等，以便联系。 6、我们保留对稿件的增删权。 7、我们对有一稿多投、剽窃或抄袭行为者，将保留追究由此引起的法律、经济责任的权利。二、投稿方式： 1、请使用电子邮件方式投递稿件。 2、编译的稿件，请注明出处并附带原文。 3、请按稿件内容投递到相关编辑信箱三、稿件著作权： 1、投稿人保证其向我方所投之作品是其本人或与他人合作创作之成果，或对所投作品拥有合法的著作权，无第三人对其作品提出可成立之权利主张。 2、投稿人保证向我方所投之稿件，尚未在任何媒体上发表。 3、投稿人保证其作品不含有违反宪法、法律及损害社会公共利益之内容。 4、投稿人向我方所投之作品不得同时向第三方投送，即不允许一稿多投。若投稿人有违反该款约定的行为，则我方有权不向投稿人支付报酬。但我方在收到投稿人所投作品10日内未作出采用通知的除外。 5、投稿人授予我方享有作品专有使用权的方式包括但不限于：通过网络向公众传播、复制、摘编、表演、播放、展览、发行、摄制电影、电视、录像制品、录制录音制品、制作数字化制品、改编、翻译、注释、编辑，以及出版、许可其他媒体、网站及单位转载、摘编、播放、录制、翻译、注释、编辑、改编、摄制。 6、投稿人委托我方声明，未经我方许可，任何网站、媒体、组织不得转载、摘编其作品。

初中数学：最短路径求最值12个模型详解，掌握了

作者:

关键词:

摘要：

获取更多教育经验、方法、学习资料等，每天与您相约！

▼

最短路径，求最值问题，已知都是考试的高频考点，而且求最值问题的各种变式题型特别多，所以，今天王老师为同学们总结了最短路径求最值12个模型概述及例题解析，对考试提分非常有帮助。

十二个基本问题概述

问题一：在直线 l 上求一点 P，使得 PA + PB 值最小 .

作法：连接 AB，与直线 l 的交点即为 P 点 .

原理：两点之间线段最短 . PA + PB 最小值为 AB .

问题二：（“将军饮马问题”）在直线 l 上求一点 P，使得 PA + PB 值最小 .

作法：作点 B 关于直线 l 的对称点 B＇，连接 AB' 与 l 的交点即为点 P．

原理：两点之间线段最短．?PA + PB 最小值为 AB' .

问题三：在直线 l1、l2 上分别求点 M、N，使得 △PMN 的周长最小．

作法：分别作点 P 关于两条直线的对称点 P' 和 P''，连接 P'P''，与两条直线的交点即为点 M，N．

原理：两点之间线段最短．?PM + MN + PN 的最小值为线段 P'P'' 的长．

问题四：在直线 l1、l2 上分别求点 M、N，使四边形 PQMN 的周长最小．

作法：分别作点 Q?、P 关于直线 l1、l2 的对称点 Q' 和 P' 连接 Q'P'，与两直线交点即为点 M，N.

原理：两点之间线段最短．?四边形 PQMN 周长的最小值为线段 Q'P' + PQ 的长．

问题五：（“造桥选址问题”）直线 m∥n，在 m、n 上分别求点 M、N，使 MN⊥m，

且 AM + MN + BN 的值最小．

作法：将点 A 向下平移 MN 的长度单位得 A'，连接 A'B，交 n 于点 N，过 N 作 NM⊥m 于 M .

原理：两点之间线段最短 . AM + MN + BN 的最小值为 A'B + MN .

问题六：在直线 l 上求两点 M , N （M 在左），使 MN = a , 并使 AM + MN + NB 的值最小 .

作法：将点 A 向右平移 a 个长度单位得 A'，作 A' 关于直线 l 的对称点 A''，连接 A''B 交直线 l 于点 N，

将 N 点向左平移 a 个单位得 M .

原理：两点之间线段最短 . AM + MN + NB 的最小值为 A''B + MN .

问题七：在 l1 上求点 A，在 l2 上求点 B，使 PA + AB 值最小 .

作法：作点 P 关于 l1 的对称点 P'，作 P'B⊥l2 于点 B，交 l1 于点 A .

原理：点到直线，垂线段的距离最短 . PA + AB 的最小值为线段 P'B 的长 .

问题八：A 为 l1上一定点，B 为 l2 上一定点，在 l2 上求点 M，在 l1上求点 N，

使 AM + MN + NB 的值最小 .

作法：作点 A 关于 l2 的对称点 A' , 点 B 关于 l1 的对称点 B'，连接 A'B' 交 l2 于点 M，交 l1 于点 N．

原理：两点之间线段最短．?AM + MN + NB 的最小值为线段 A'B' 的长．

问题九：在直线 l 上求一点 P，使 | PA - PB | 的值最小．

作法：连接 AB，作 AB 的中垂线与直线 l 的交点即为 P 点．

原理：垂直平分上的点到线段两端点的距离相等． | PA - PB | = 0 .

问题十：在直线 l 上求一点 P，使 | PA - PB | 的值最大．

作法：作直线 AB，与直线 l 的交点即为 P 点．

原理：三角形任意两边之差小于第三边． | PA - PB | ≤ AB ， | PA - PB | 的最大值 = AB .

问题十一：在直线 l 上求一点 P，使 | PA - PB | 的值最大．

作法：作点 B 关于直线 l 的对称点 B' 作直线 AB'，与直线 l 的交点即为 P 点．

原理：三角形任意两边之差小于第三边． | PA - PB | ≤ AB' ， | PA - PB | 的最大值 = AB' .

问题十二：（“费马点”）△ABC 中每一内角都小于 120°，在 △ABC 内求一点 P，

使得 PA + PB + PC 的值最小 .

作法：所求点为 “费马点” ，即满足 ∠APB = ∠BPC = ∠APC = 120° .

以 AB 、 AC 为边向外作等边 △ABD、△ACE，连接 CD、BE 相交于点 P，点 P 即为所求 .

原理：两点之间线段最短 . PA + PB + PC 的最小值 = CD .

费马点

— 到三点距离之和最小的点

费马点的构造方法：

① 所给三点的连线构成三角形（△ABC），并且这个三角形的每个内角都小于 120°；

② 如下图所示：A , B , C 是给定的三点，

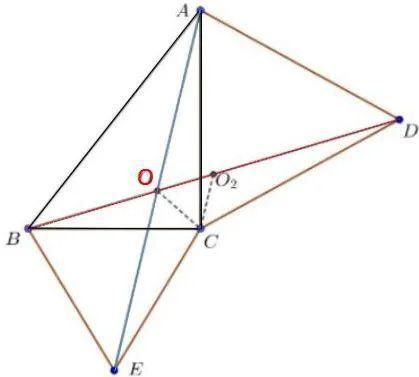以 AC 为边向外作正三角形得到点 D , 以 BC 为边向外作正三角形得到点 E ,

连接 BD 和 AE 交于点 O，我们断言点 O 就是 “费马点” .

费马点的证明方法：

先证 △AEC ≌ △DBC .

△AEC 绕点 C 顺时针旋转 60°，可得到 △DBC，从而 △AEC ≌ △DBC .

于是 ∠OBC = ∠OEC，所以 O、B、E、C 四点共圆 .

拓展知识：四点共圆判定方法

若线段同侧二点到线段两端点连线夹角相等，那么这二点和线段二端点四点共圆 .

所以 ∠BOE = ∠BCE = 60°，∠COE = ∠CBE = 60°，

于是 ∠BOC = ∠BOE + ∠COE = 120°，同理可证 ∠AOC = ∠AOB = 120°，

文章来源：《数学教育学报》网址: http://www.sxjyxbzz.cn/zonghexinwen/2021/0313/646.html